Logaritmacion

En análisis matemático, usualmente, el logaritmo de un número real positivo —en una base de logaritmo determinada— es el exponente al cual hay que elevar la base para obtener dicho número. Por ejemplo, el logaritmo de 1000 en base 10 es 3, porque 1000 es igual a 10 a la potencia 3: 1000 = 10³ = 10×10×10.

De la misma manera que la operación opuesta de la suma es la resta y la de la multiplicación la división, el cálculo de logaritmos es la operación inversa a la exponenciación de la base del logaritmo.

Para representar la operación de logaritmo en una determinada base se escribe la abreviatura log y como subíndice la base y después el número resultante del que deseamos hallar el logaritmo. Por ejemplo, 3⁵=243 luego log₃243=5. Cuando se sobreentiende la base, se puede omitir.

Los logaritmos fueron introducidos por John Napier a principios del siglo XVII como un medio de simplificación de los cálculos. Estos fueron prontamente adoptados por científicos, ingenieros, banqueros y otros para realizar operaciones fácil y rápidamente, usando reglas de cálculo y tablas de logaritmos. Estos dispositivos se basan en el hecho más importante — por identidades logarítmicas — que el logaritmo de un producto es la suma de los logaritmos de los factores:

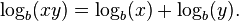
Si los números a y b son positivos, b la base diferente a 1 y a 0. Se dirá que el logaritmo de a en la base b es h si se cumple que

, y se denota 

• Logaritmo puede ser definido de diversas maneras: como exponente, cuando se conocen la base de una potencia y el valor de esta; tal el caso si

, como  resuelve la ecuación, se dice que -4 es el logaritmo de 1/16 en base 2. O bien

.¹ .

Se exige que la base de logaritmos sea un número positivo distinto de 1. Usualmente se ha considerado como base, 10: originando los logaritmos decimales o vulgares. O bien la base, el número e: generando los logaritmos naturales o neperianos.

• Como una función real de variable real. Concretamente, considerando que la función exponencial es una función creciente y continua de dominio ℝ y codominio ℝ⁺, pues tiene función inversa de dominio ℝ⁺, y codominio ℝ, que también es creciente y continua para base mayor que 1.²
• Por integral definida

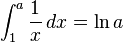que se lee logaritmo natural de a, en este caso la base de los logaritmos es el número irracional trascendente e que es el límite de

cuando n tiende a infinito.³

Dado un número real (argumento x), la función logaritmo le asigna el exponente n (o potencia) a la que un número fijo b (base) se ha de elevar para obtener dicho argumento. Es la función inversa de b a la potencia n. Esta función se escribe como: n = log_b x, lo que permite obtener n.⁴

(esto se lee como: logaritmo en base b de x es igual a n; si y sólo si b elevado a la n da por resultado a x)

Para que la definición sea válida, no todas las bases y números son posibles. La base b tiene que ser positiva y distinta de 1, luego b> 0 y b ≠ 1, x tiene que ser un número positivo x > 0 y n puede ser cualquier número real (n ∈ R).⁵

Así, en la expresión 10² = 100, el logaritmo de 100 en base 10 es 2, y se escribe como log₁₀ 100=2.