La factorización es una técnica que consiste en la descripción de una expresión matemática (que puede ser un número, una suma, una matriz, un polinomio, etc.) en forma de producto. Existen distintos métodos de factorización, dependiendo de los objetos matemáticos estudiados; el objetivo es simplificar una expresión o reescribirla en términos de «bloques fundamentales», que reciben el nombre de factores, como por ejemplo un número en números primos, o un polinomio en polinomios irreducibles.
El teorema fundamental de la aritmética cubre la factorización de números enteros, y para la factorización de polinomios, el teorema fundamental del álgebra. La factorización de números enteros muy grandes en producto de factores primos requiere de algoritmos sofisticados, el nivel de complejidad de tales algoritmos está a la base de la fiabilidad de algunos sistemas de criptografía asimétrica como el RSA.
Factorizar un polinomio
Una factorización de un polinomio de grado n es un producto de como mucho </math> \scriptstyle m \le n factores o polinomios de grado\scriptstyle n_k \le n</ con \scriptstyle 1 \le k \le m</math>. Así por ejemplo el polinomio P(x) de grado 5 se puede factorizar como producto de un polinomio de grado 3 y un polinomio de grado 2:
P(x) = x^5-x^3+69x^2-20x+16 = (x^3+4x^2-x+1)(x^2-4x+16)\
Factor Común Monomio
Se trata de extraer de un polinomio, un monomio como factor común a cada uno de los términos del polinomio en cuestión. El procedimiento empieza por extraer el Máximo Común Divisor (M.C.D.) de los coeficientes del polinomio de esta manera. Ejemplo:
12y^3 x^2 + 30x^5 y^3 - 18m^3 x y^4
Los coeficientes sin sus respectivos signos son: 12, 30 y 18. El M.C.D. de ellos es 6, luego dividimos cada uno de los coeficientes entre el número 6 por lo tanto se puede expresar que:

Luego debemos identificar que variables o literales poseen en común todos los términos, y observamos que todos los términos cuentan con las variables "x" e "y", excepto "m" que no está en todos. Luego de identificar la variables comunes debemos observar cual es el menor exponente al que esta elevada la variable en los términos en cuestión; y podemos observar que el exponente menor de "x" es 1 y el menor exponente de "y" es 3. Por lo tanto podemos extraer como factor común también a  . Para hacerlo debemos dividir cada término entre
. Para hacerlo debemos dividir cada término entre  . Quedando la expresión factorizada de la siguiente forma:
. Quedando la expresión factorizada de la siguiente forma:
 . Para hacerlo debemos dividir cada término entre
. Para hacerlo debemos dividir cada término entre  . Quedando la expresión factorizada de la siguiente forma:
. Quedando la expresión factorizada de la siguiente forma:
Factorización por Agrupación de Términos
La factorización por agrupación de términos puede utilizarse en polinomios con un número de términos par y mayor o igual a 4. Debe buscarse en este caso de factorización parejas de términos que tengan en común un factor. Ejemplo:

Observamos por ejemplo que podemos agrupar los términos  , y
, y  porque poseen en común la "y", y sobran los términos
porque poseen en común la "y", y sobran los términos  y
y  que tienen también en común la "p". Quedando expresado de la siguiente forma:
que tienen también en común la "p". Quedando expresado de la siguiente forma:
 , y
, y  porque poseen en común la "y", y sobran los términos
porque poseen en común la "y", y sobran los términos  y
y  que tienen también en común la "p". Quedando expresado de la siguiente forma:
que tienen también en común la "p". Quedando expresado de la siguiente forma:
Luego se saca el factor común de ambos, así:

Luego observamos las expresiones que se encuentran dentro del paréntesis las cuales si las reordenamos según la propiedad conmutativa para suma, obtendremos lo siguiente:

Se observa de nuevo que está en común el factor  , luego también puede sacarse como factor común a ambas expresiones o agrupaciones de términos, quedando al final la factorización así:
, luego también puede sacarse como factor común a ambas expresiones o agrupaciones de términos, quedando al final la factorización así:
 , luego también puede sacarse como factor común a ambas expresiones o agrupaciones de términos, quedando al final la factorización así:
, luego también puede sacarse como factor común a ambas expresiones o agrupaciones de términos, quedando al final la factorización así:
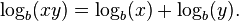
 , y se denota
, y se denota 
 , como
, como  resuelve la ecuación, se dice que -4 es el logaritmo de 1/16 en base 2. O bien
resuelve la ecuación, se dice que -4 es el logaritmo de 1/16 en base 2. O bien .
.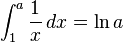












 el denominador "b" expresa la cantidad de partes iguales que representan la unidad, y el numerador "a" indica cuántas de ellas se toman.
el denominador "b" expresa la cantidad de partes iguales que representan la unidad, y el numerador "a" indica cuántas de ellas se toman.









 .
. .
.